Największy wspólny dzielnik (NWD) dwóch liczb całkowitych – jak obliczyć
Obliczenie największego wspólnego dzielnika można wykonać za pomocą dwóch sposobów. Należą do nich: obliczanie NWD dwóch liczb całkowitych przy pomocy algorytmu Euklidesa oraz z użyciem rozkładu liczb całkowitych na czynniki pierwsze.
Algorytm Euklidesa – jak znaleźć największy wspólny dzielnik
Oto jak działa algorytm Euklidesa:
- Podziel większą liczbę przez mniejszą.
- Zapisz resztę z tego dzielenia.
- Zastąp większą liczbę mniejszą liczbą, a mniejszą liczbą resztą.
- Powtarzaj te kroki, aż reszta stanie się zerem.
- Największy wspólny dzielnik to ostatnia niezerowa reszta.
Przykład:
Obliczmy NWD dla liczb 48 i 18:
- Liczbę 48 dzielimy przez 18, reszta to 12 (48 = 18 * 2 + 12).
- Teraz bierzemy liczby 18 i 12. Dzielimy 18 przez 12, reszta to 6 (18 = 12 * 1 + 6).
- Następnie bierzemy liczby 12 i 6. Dzielimy 12 przez 6, reszta to 0 (12 = 6 * 2 + 0).
- Ze względu na to, że reszta wynosi 0, zatrzymujemy się. Ostatnia niezerowa reszta to 6.
Zatem największym wspólnym dzielnikiem liczb 48 i 18 jest 6. NWD (48, 18) = 6.
Rozkład liczb na czynniki pierwsze – inny sposób, jak obliczyć NWD
Największy wspólny dzielnik (NWD) dwóch liczb całkowitych można obliczyć także przy pomocy rozkładu na czynniki pierwsze. Czynnik pierwszy to dowolna liczba pierwsza, która dzieli bez reszty daną liczbę naturalną złożoną. Z kolei liczba pierwsza to liczba naturalna większa od 1, która ma dokładnie dwa dzielniki naturalne: jedynkę i siebie.
-
Rozkład na czynniki pierwsze – najpierw należy rozłożyć obie liczby na czynniki pierwsze. Na przykład, dla liczb 60 i 48 mamy:
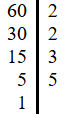
- Porównanie czynników – należy przeanalizować wspólne czynniki pierwsze obu liczb.
- Znalezienie tych samych czynników – wypisujemy te czynniki, które powtórzyły się w obu rozkładach (każdy czynnik tylko raz).
- Obliczenie NWD – pomnóż te wspólne czynniki pierwsze. Wynik będzie największym wspólnym dzielnikiem.
Przykład dla liczb 60 i 48:
- czynnikami pierwszymi 60 są: 2, 2, 3 i 5,
- czynnikami pierwszymi 48 są: 2, 2, 2, 2 i 3.
Wspólne czynniki pierwsze: 2, 2 i 3.
Teraz liczymy największy wspólny dzielnik: NWD (60, 48) = 2 x 2 x 3 = 12.
Zatem największy wspólny dzielnik liczb 60 i 48 to 12. NWD (60, 48) = 12.
Największy wspólny dzielnik – wiedza w pigułce
Największy wspólny dzielnik (NWD) to największa liczba, która dzieli jednocześnie dwie lub więcej liczb całkowitych bez reszty. NWD jest istotnym pojęciem w matematyce, a jego znajomość ma praktyczne zastosowanie w wielu dziedzinach, takich jak arytmetyka, algebra czy rozwiązywanie równań.
Istnieje kilka metod obliczania NWD, jednak na poziomie szkoły podstawowej i ponadpodstawowej najlepiej sprawdzają się dwie metody:
- Metoda rozkładu na czynniki pierwsze – polega na rozłożeniu liczb na czynniki pierwsze i wybieraniu tych, które występują w obu rozkładach, z najmniejszymi wykładnikami, a następnie ich wymnożeniu.
- Algorytm Euklidesa – jest to metoda, która wykorzystuje właściwość dzielenia z resztą. Proces ten powtarza się, aż jedna z liczb stanie się zerem. Wówczas wyznaczamy NWD.
W praktyce, obliczanie największego wspólnego dzielnika można przeprowadzić ręcznie lub za pomocą kalkulatorów oraz programów komputerowych, które automatyzują ten proces.