Dodawanie i odejmowanie ułamków zwykłych to jedna z podstawowych operacji matematycznych, z którą mamy do czynienia w matematyce. Ułamki są niezwykle ważne, ponieważ pojawiają się w większości działów. W artykule tym przyjrzymy się szczegółowo, jak skutecznie odejmować ułamki, zarówno te o wspólnych mianownikach, jak i te, które posiadają odmienne mianowniki. Zrozumienie tej tematyki pozwoli nie tylko na szybkie rozwiązywanie zadań matematycznych, ale także na pewniejsze poruszanie się w świecie liczb i proporcji. Poniżej przedstawimy kilka praktycznych przykładów wraz z rozwiązaniami oraz jedno zadanie tekstowe z wykorzystaniem odejmowania ułamków.
Odejmowanie ułamków zwykłych – wyjaśnienie i przykłady
Spis treści
Ułamki zwykłe o jednakowych mianownikach – odejmowanie
Odejmowanie ułamków o tych samych mianownikach jest prostą sprawą. Wystarczy odjąć licznik (na górze) jednego ułamka od licznika drugiego ułamka, a mianownik pozostaje ten sam.
Poniżej przykład jak wykonać takie działanie:
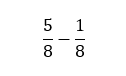
- Sprawdź mianowniki – oba ułamki mają ten sam mianownik, którym jest 8.
- Odejmij liczniki – teraz odejmujemy licznik pierwszego ułamka od licznika drugiego:
5 - 1 = 4.
- Zachowaj mianownik – mianownik pozostaje taki sam, czyli 8.
- Zapisz wynik – ostateczny wynik odejmowania to:
-
Skróć ułamek – jeśli się da, należy skrócić (czyli podzielić licznik i mianownik przez największy wspólny dzielnik – najwyższą liczbę, przez którą dzieli się, w tym przypadku, 4 i 8) ułamek do ułamka nieskracalnego:
Podsumowując:
Warto pamiętać, że wynikiem odejmowania ułamków o tym samym mianowniku jest ułamek, którego mianownik jest identyczny, a licznik to różnica liczników.
Odejmowanie ułamków o różnych mianownikach – wytłumaczenie z przykładem
Odejmowanie ułamków zwykłych o różnych mianownikach wymaga najpierw sprowadzenia ich do wspólnego mianownika (najmniejszej wspólnej liczby, przez którą dzielą się oba mianowniki).
Poniżej przykład takiego działania:
- Znajdź wspólny mianownik – mianowniki to 6 i 4. Wspólnym mianownikiem dla 6 i 4 jest 12.
- Sprowadzanie ułamków do wspólnego mianownika – w pierwszym ułamku robimy działanie 12:6, a następnie mnożymy licznik przez wynik, czyli 5*2. Licznik pierwszego ułamka to 10. W drugim ułamki robimy działanie 12:4, a wynik mnożymy przez licznik, czyli 3*3. Licznik w drugim ułamku wynosi 9:
-
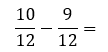
Odejmij ułamki – ze względu na wspólny mianownik, po prostu odejmujemy liczniki:
10 - 9 = 1
- Zapisz wynik:
Wynik odejmowania to:
Podsumowując:
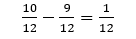
Zadanie tekstowe z użyciem ułamków zwykłych
Poniżej przykładowe zadanie tekstowe z odejmowaniem ułamków zwykłych oraz jego rozwiązanie.
Zadanie. Po imprezie urodzinowej Kasia włożyła do lodówki 3/4 tortu czekoladowego. W nocy Kasia miała ogromną chęć na zjedzenie trochę ciasta. Po skonsumowaniu tortu przez Kasię, w lodówce zostało 1/2 ciasta. Ile tortu Kasia zjadła w nocy?
Rozwiązanie – aby znaleźć ilość tortu, która została zjedzona, musimy od początkowej ilość tortu (3/4) odjąć wartość, która została (1/2).
Musimy wykonać działanie:
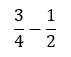
Aby odjąć te dwa ułamki, najpierw musimy doprowadzić je do wspólnego mianownika. Mianownikiem dla 4 i 2 jest 4. Oby dwa ułamki należy przekształcić, aby miały mianownik 4 i odpowiednie liczniki:
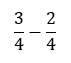
Teraz możemy odjąć ułamki:
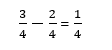
Odpowiedź: Kasia zjadła w nocy 1/4 tortu.
Podsumowanie wiadomości o odejmowaniu ułamków zwykłych
Odejmowanie ułamków zwykłych to proces, który można podsumować w kilku krokach. Oto podstawowe zasady tego działania:
- Ułamki o tym samym mianowniku – w przypadku gdy dwa ułamki mają ten sam mianownik, odejmujemy tylko liczniki, zachowując wspólny mianownik.
- Ułamki o różnych mianownikach – w takiej sytuacji należy najpierw znaleźć wspólny mianownik, który jest najmniejszą wspólną wielokrotnością (NWW) mianowników. Następnie należy przekształcić ułamki tak, aby miały ten sam mianownik i odpowiedni licznik, a następnie wykonać odejmowanie liczb.
- Uproszczenie ułamka – po wykonaniu odejmowania warto sprawdzić, czy ułamek z wyniku można uprościć, dzieląc licznik i mianownik przez ich największy wspólny dzielnik (NWD).
To ogólne zasady, które pomogą w odejmowaniu ułamków zwykłych. W praktyce warto ćwiczyć różne przykłady, aby nabrać biegłości w zakresie działań na ułamkach, które są podstawą do dalszych matematycznych zadań obliczeniowych.
Bibliografia
- https://www.matemaks.pl/dodawanie-i-odejmowanie-ulamkow-zwyklych.html.
- Odejmowanie ułamków zwykłych – Medianauka.pl.
- Zintegrowana Platforma Edukacyjna (zpe.gov.pl).
Opublikowano: 08.10.2024;
Oceń:
4.0
Komentarze i opinie (0)