Zamiana ułamków zwykłych na dziesiętne – wyjaśnienie i przykłady

Jak przekształcić ułamki zwykłe na ułamki dziesiętne – przykłady

Pierwszy sposób zamiany ułamków zwykłych na dziesiętne

Aby zamienić ułamek zwykły na dziesiętny, należy podzielić licznik przez mianownik. Ułamek w postaci x/y można przekształcić w postać dziesiętną poprzez wykonanie dzielenia pisemnego x : y.

Przykład 1. Zamieńmy ułamek 3/4 na ułamek dziesiętny.

• Licznik i mianownik – w tym przypadku licznik to 3, a mianownik to 4.
• Dzielenie – wykonujemy dzielenie:

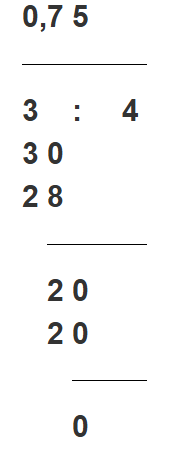
• Wynik: Ułamek 3/4 w postaci dziesiętnej to 0,75.

Podsumowanie:

Aby zamienić ułamek zwykły na dziesiętny, wykonujemy dzielenie licznika przez mianownik. W przypadku 3/4 wynikiem jest 0,75.

Przykład 2. Zamieńmy ułamek 1/5 na ułamek dziesiętny.

• Licznik i mianownik – w tym przypadku licznik to 1, a mianownik to 5.
• Dzielenie – wykonujemy dzielenie:

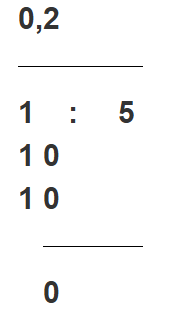
• Wynik: Ułamek 1/5 w postaci dziesiętnej to 0,2.

Podsumowanie:

Aby zamienić ułamek zwykły na dziesiętny, wykonujemy dzielenie licznika przez mianownik. W przypadku 1/5 wynikiem jest 0,2.

Drugi sposób zamiany ułamków zwykłych na dziesiętne

Aby zamienić ułamek zwykły na dziesiętny, można sprawdzić, czy mianownik tego danego da się rozszerzyć do 10, 100 lub ewentualnie 1000. Za przykład może posłużyć powyższe działanie. Aby zamienić ułamek 1/5 na ułamek dziesiętny, jednym ze sposobów jest podzielenie licznika przez mianownik (jak zrobiliśmy wyżej). Drugi natomiast sposób to rozszerzenie mianownika tego ułamka (do 10, 100, 1000). W tym przypadku mianownik 5 można rozszerzyć do 10. Skoro rozszerzyliśmy mianownik, należy też rozszerzyć licznik. Jako że mianownik, aby uzyskać 10, pomnożyliśmy przez 2, licznik również należy pomnożyć przez 2. I tym samym wychodzi nam wynik 2/10, czyli 0,2.

Rozwinięcie dziesiętne ułamków nieskończonych

Aby przekształcić ułamek na liczbę dziesiętną, należy wykonać dzielenie liczby w liczniku (górna część ułamka) przez liczbę w mianowniku (dolna część ułamka). Poniżej przykład krok po kroku:

• Wykonaj dzielenie – podziel licznik przez mianownik.
• Zanotuj wyniki – w przypadku, gdy obliczenia się nie kończą, zapisujemy ułamek w tzw. okresie. Okres to powtarzająca się w ułamku dziesiętnym liczba (lub liczby). W naszym przypadku będzie to 3. Okres zapisujemy w nawiasie.

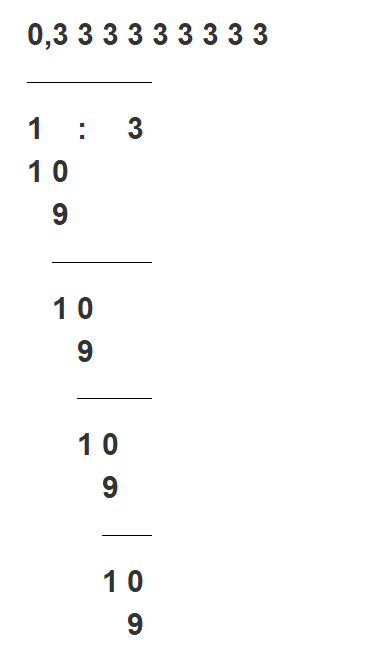
• Zapisz wynik – dzielenie pisemne daje nieskończony wynik, który można zapisać jako 0,(3).

Podsumowanie:

Ułamek zwykły można przekształcić na dziesiętny przez dzielenie, a wynik może być liczbą dziesiętną niekończącą się.

Podsumowanie wiadomości na temat zamiany ułamków z kreską na ułamki z przecinkiem

Przekształcanie ułamków zwykłych w ułamki dziesiętne polega na dzieleniu liczników przez mianowniki lub rozszerzeniu mianownika ułamka zwykłego do 10, 100 lub 1000. Oto najważniejsze informacje na ten temat:

1. Ułamek właściwy – gdy licznik jest mniejszy od mianownika, dzielenie daje wynik mniejszy od 1. Przykład: 2/5 = 0,4.
2. Ułamek niewłaściwy – gdy licznik jest większy lub równy mianownikowi, dzielenie może dać wynik równy lub większy od 1. Przykład: 1 i 1/4 = 1,25.
3. Ułamek skończony – ułamek, który po przekształceniu daje skończony ułamek dziesiętny. Przykład: 3/8 = 0,375.
4. Ułamek nieskończony okresowy – ułamek, który po przekształceniu daje nieskończony ułamek dziesiętny. Przykład: 2/3 = 0,(6).

Zrozumienie tych zasad pozwala na skuteczne przekształcanie ułamków zwykłych na dziesiętne w różnych działaniach matematycznych.